Kyuho's personal homepage

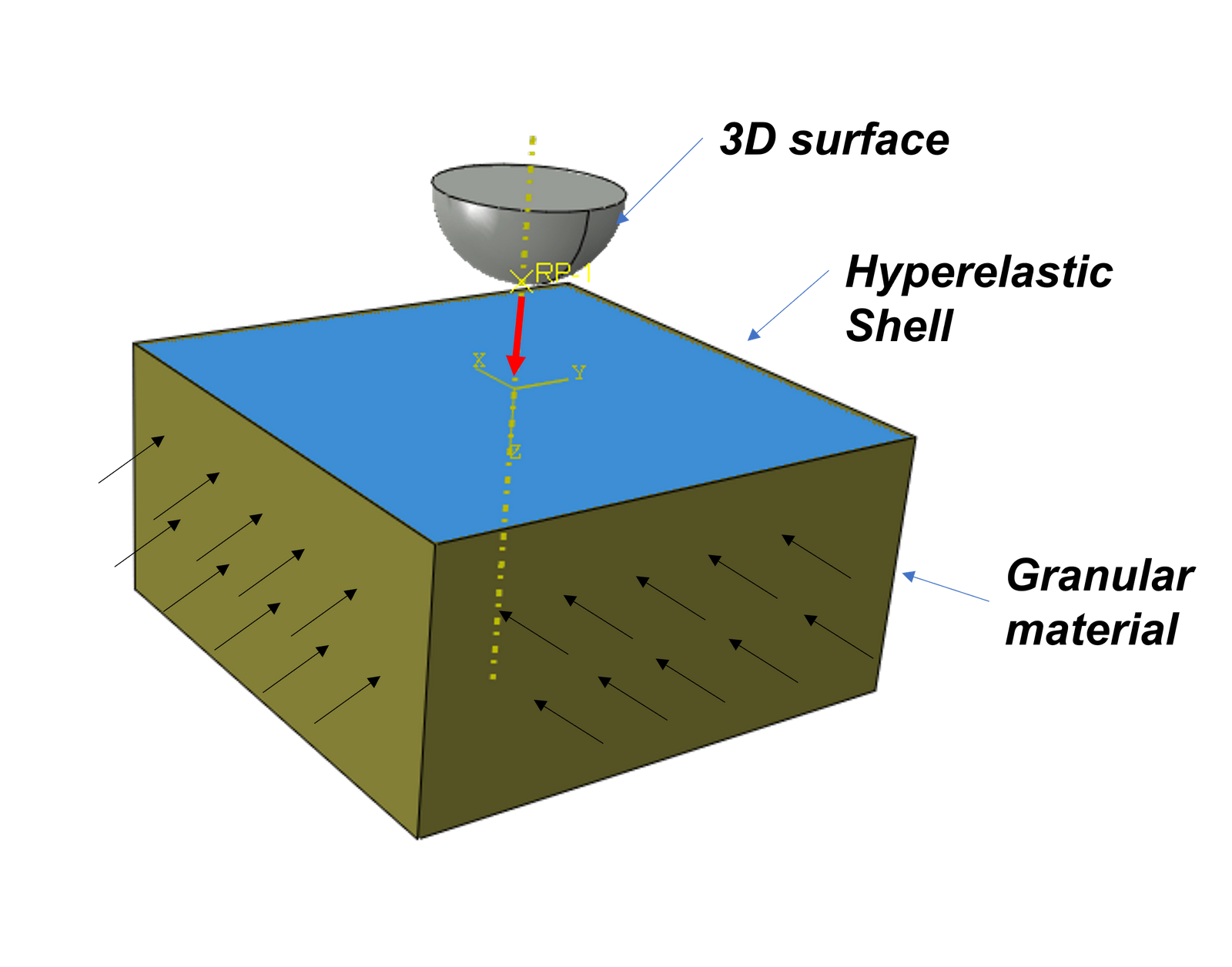
Powder Transfer Printing using Computational Method

Backgrounds and Motivations

Soft Robotics is in the spotlight because it can perform a unique skill that “hard” robots can’t.
However, an accurate sensor locating technique is necessary for advanced soft robots, which is very hard because of their complex surface.

Figure 1. Examples of soft robotics

Water Transfer Printing (WTP) is a well-known technology for transferring color images to a 3D surface.  
Recently, WTP technique was suggested as a solution to sensor locating problems in soft robotics (Borgne et al., ACS 2017). 

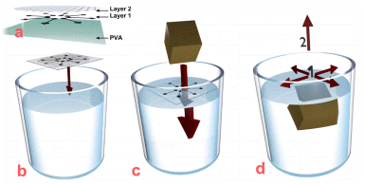
Figure 2. water transfer printing technology in manufacturing of conformal electronics (Borgne et al. ACS 2017)

However, this technology has a significant problem. The position of sensors or circuits on the water varies with time.
This problem occurs due to the instability and surface tension of water.

Figure 3. Disadvantages of water

Therefore, we solved the problem by replacing water with granular materials and named it "powder transfer printing".
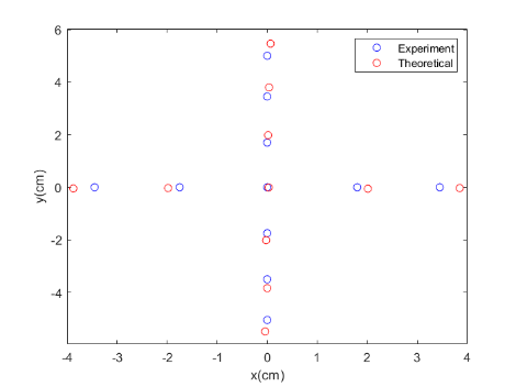
Also, we adapted a computational method to improve precision of sensors' location after transfer printing. 

First, we replaced water with granular materials. Granular materials easily deform and show almost perfect plastic behavior, so they are an ideal substitute for water. Also, granular materials have negligible surface tension and are much more stable than water, so using these would not show the problem mentioned above.  

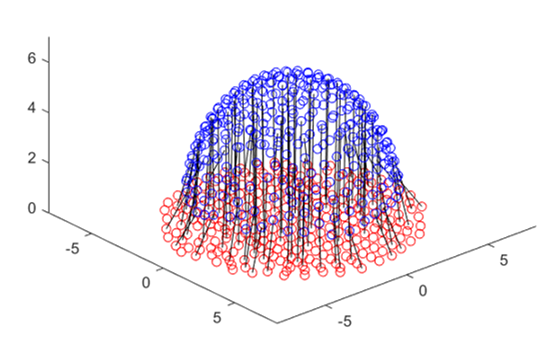
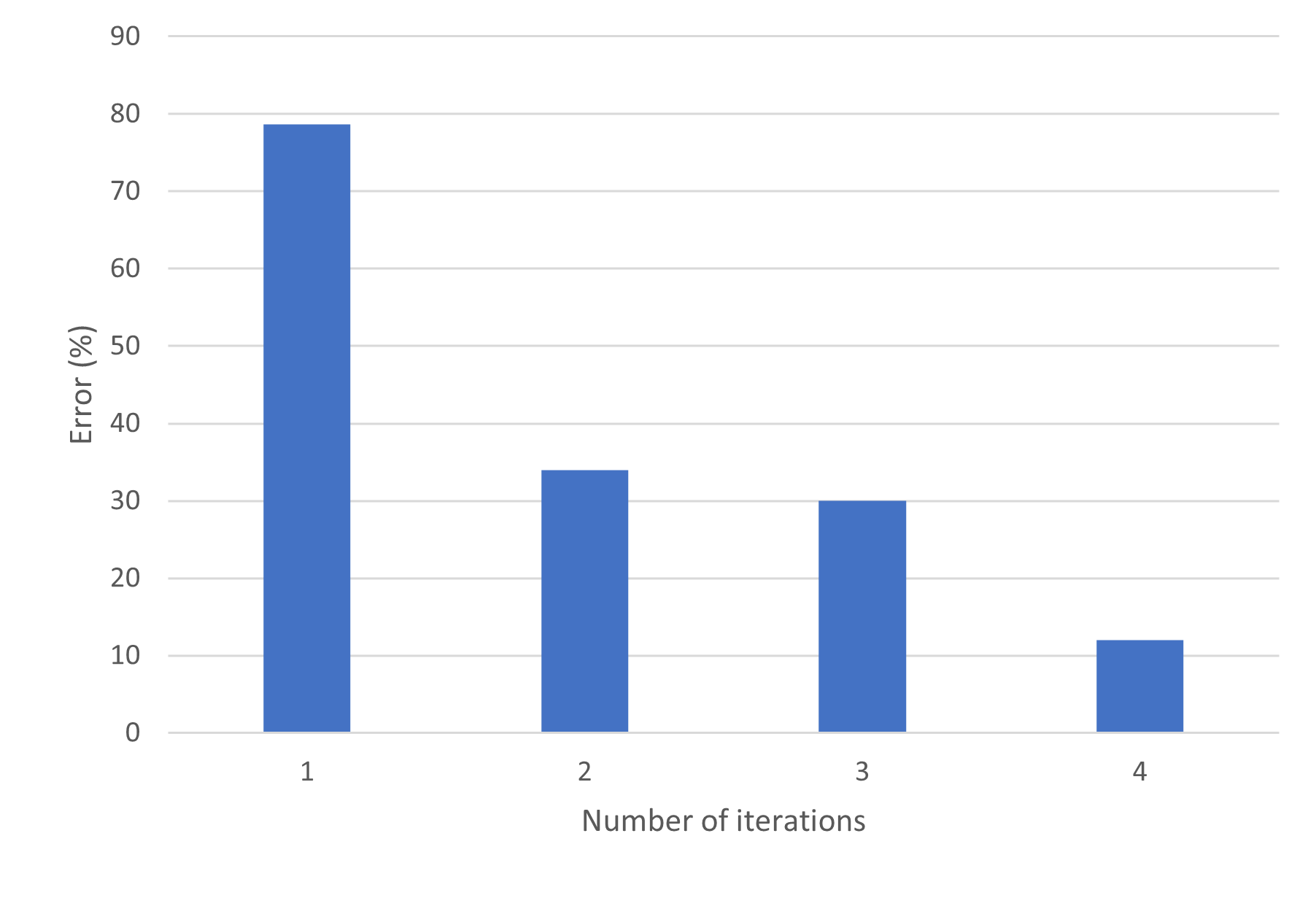
Second, we adapted the computational method. Zhang et al. have already developed a computational method for WTP. However, the response of granular materials to stress is more complex than water. So we devised a new methodology to computationally predict the sensors' location after transfer printing. 

Methodology

Figure 4. schematics of powder transfer printing

The above figure describes the schematics of powder transfer printing. 
First, a hyperelastic shell is placed on top of the granular material. Then, a complex-shaped 3D surface is transferred into the granular material with constant speed.

Figure 5. Overall algorithm for precisely locating sensors on complex 3D surface

The above algorithm is the overall algorithm for precisely locating sensors on conformal electronics.
To test the validity of the algorithm, we performed a simple experiment.
First, we designed sensor patterns on the sphere surface.

Sensor location

  • Azimuthal angle: 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°
  • Altitude angle: 0°, 22.5°, 45°, 67.5°
  • Radius of sensors: 0.25 cm
  • Radius of the spehre: 5 cm

Blue: sensors
Red: 3D surface (sphere)

Figure 6. Sensor design on sphere 

Then, we ran the algorithm. The error used in the algorithm is expressed as follows:

\[Err = \sqrt{\sum_{i = 1}^{N}{(r_{i,theo}-r_{i,simul})^2}}\]

where \(N\) is a total number of sensors, \(r_{i,theo}\) is a intended sensor location and \(r_{i,simul}\) is a simulated sensor location

After obtaining the exact location of sensors, we performed a powder transfer printing on a 3D-printed sphere to validate our algorithm.

Figure 7. Experiment apparatus

Result and Discussion

Red: hyperelastic shell
Blue: sphere

Figure 8. A contact map between a sphere and a hyperelastic shell

Figure 8 describes a map created by the algorithm introduced in Figure 5.
Red dots represent nodes in the hyperelastic shell, and blue dots represent nodes in the 3D surface, which is the sphere. 
Black lines connect nodes that are in contact with each other during transfer printing.

Figure 9. Comparison between experiment result and the original design.

The average distance between the design and the experiment result was 0.1 cm.
The error might be originated from the error of material properties in the simulation, so the exact material properties are required for high accuracy
 

Figure 10. number of algorithm iterations vs error (%) 

\(Err (\%) = {\sqrt{\sum_{i = 1}^{N}{(r_{i,theo}-r_{i,simul})^2}}\over{R}}\)

where \(R\) is a radius of sensor (here, \(R\)=0.25 cm)

Figure 10 describes the decreasing tendency in error while the algorithm proceeded.
Error percent reached about 10% after only four iterations in this Figure, proving the validity of the proposed algorithm. 

Conclusion

Long story short, this study shows that powder transfer printing could be used in the manufacturing of conformal electronics.
The result of the simulation and experiment shows the possibility that our methodology is adequate for locating the sensors.
The convergence of the proposed algorithm is proved by Figure 10.

However, the experiment result was different from the simulation result about 10%, which was due to the error in material properties.

Future Works